Generating and solving sudoku puzzles

Mar 14, 2010

My fascination of sudoku started when I was working down the family store; one of my coworkers would do sudoku puzzles during quiet periods. He showed me how to play and I started to wonder how people would actually create the puzzles. I figured that the easiest approach would be to start with a completed grid and then remove as many numbers as possible.

Using javascript I defined a data structure that allowed me to interact with the grid in any way that I could possibly need to. So iterating cells along rows, columns, blocks, setting flags on each of these things, etc. Output was presented using HTML and CSS although I didn’t add any input support other than through the browser console.

Solving puzzles

I implemented a solver using the strategy design pattern where each solving technique is implemented as a separate strategy class. Strategies can then be applied to not only solve a puzzle but to approximate it’s difficulty and provide an estimated solution time.

I was able to fine tune the estimated solution time using the average completion times of some friends who played a selection of my generated puzzles.

The meat and bones of the solver follows this logic:

// Assume easiest difficulty and then refine throughout process.
int difficulty = Puzzle.NOVICE;
int iterationCount = 0;

// Try using each strategy using the simplest where possible.
while (incomplete) {
    progressMade = false;
    ++iterationCount;

    for (int i = 0; i < strategies.length; ++i) {
        var strategy = strategies[i];
        strategy.searchPuzzle(puzzle);
        if (progressMade) {
            // Update estimated difficulty metric.
            difficulty = max(difficulty, strategy.getDifficulty());
            // Break on progress to try simpler strategies again!
            break;
        }
        else {
            // If no progress has been made, bail :(
            return null;
        }
    }
}

High level process

The basic high level process that I came up with is:

1. Generate a completed puzzle.

2. Create an empty puzzle and copy a predetermined minimum number of hints from the completed grid using an abstraction that copies hints with the active symmetry. Copying with symmetry makes for more visually appealing puzzles.

3. I then initialize a solver registering strategies of the desired difficulty along with a special “correction” strategy. The correction strategy is the absolute last resort which cheats by copying an additional hint from the completed grid (again using symmetry). The correction strategy tries to place the least useful hint.

4. At this stage the solvable puzzle tends to be considerably easier than the desired difficulty. So the puzzle is reduced by removing as many hints as possible whilst still yielding a solvable puzzle.

5. If the reduced puzzle still isn’t difficult enough then the puzzle is erased and the previous two steps are repeated several times from the same completed grid. If a puzzle cannot be generated after several iterations then the entire process will restart by generating a new completed grid. I found that some completed grids do not lead to desirable puzzles until after a considerable number of iterations so it’s more efficient to just pass on those ones.

Generating the completed puzzle

This was perhaps the most challenging aspect of the project because every time that I thought that I finally had a decent approach… I would bump into a completely impossible grid with empty cells.

The simplest approach was simply transpose an already completed sudoku grid and then randomly swap the digits. The problem with this approach was that somehow the grid felt too familiar after a while. I felt that I could do a lot better than this.

Whilst my coworker was solving the sudoku puzzles in his book I was solving completely empty grids on paper. Eventually I came up with a solution that will produce a random completed grid. On the rare occasions where an impossible grid occurs it will simply repeat the process again. After stress testing the generation of thousands of grids I found that no single grid exceeded 3 generation iterations.

The first step is to fill each cell of the center block of the grid randomly. The center row and column can then be completed at random:

The first row of the central chunk can then be filled in by prioritizing the placement of numbers that would be impossible to place on the opposite sides (green = numbers that have to be placed, blue = prioritized, red = entirely random). The exact same approach can then be applied to the last row of the central block and for the two incomplete columns of the central blocks:

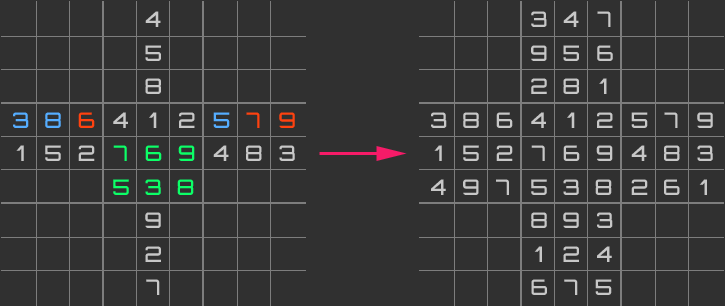
Empty cells are then filled by adding the “pencil marks” to all of the cells and then filling in all cells that only have 1 possible value. If this is not possible then a guess must be made. Each block must be processed in a queued order (either clockwise or counter- clockwise). The first cell that has the fewest number of candidate values is chosen and a candidate is chosen at random.

With this particular puzzle 4 guesses had to be made; I have color coded the following illustration so that you can see how many cells became solvable after guessing a single cell: